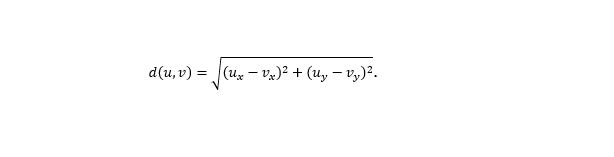1 Introduction

Flooding is a simple broadcast protocol for delivering a message to all nodes in a network. Many routing protocols for mobile ad hoc networks (MANETs), such as Ad-hoc On-Demand Distance Vector (AODV), Dynamic Source Routing (DSR), Zone Routing Protocol (ZRP), and Location-Aided Routing (LAR), use flooding as the basic mechanism to disseminate or to propagate route discovery control messages (Perkins, 2001; Abolhasan, 2004; Perkins, 2003; Rendong, 2006; Haas, 1997; Ko, 2000). An efficient flooding scheme is therefore useful to reduce the overhead of such routing protocols, decrease collisions, and improve network throughput. The simplest flooding technique, called pure flooding or blind flooding, is first discussed in Ho (1999). In this scheme, every node in the network retransmits a received broadcast message, when it receives this message for the first time. Despite its simplicity and guarantee that a flooding message can reach all nodes (if there are no collisions and the network is connected), pure flooding generates an excessive amount of redundant network traffic, because it requires every node to retransmit the message. Due to the broadcast nature of radio transmissions, when all nodes transmit a message in the network, there is a very high probability of signal collisions (Sinha, 2001). It may cause some nodes to fail to receive the flooding message. This is the so-called broadcast storm problem (Ni, 1999).

Existing efficient flooding schemes can be classified into three categories based on the information each node keeps: 1) no need of neighbour information, 2) keeping 1-hop neighbour information, or 3) keeping 2-hops neighbour information and more (Liu, H., 2007). We focus on the second category, where each node keeps 1-hop neighbour geographical location information. The authors in Liu, H. et al. (2007) distinguish algorithms in this category based on sender-based and receiver-based strategies, while the authors in Khabbazian & Bhargava (2008) term them as neighbour-designing and self-pruning algorithms, respectively. In a sender-based strategy, each node schedules a broadcast for a received flooding message if the node is selected by the sender and if it has not previously received this message. In a receiver-based strategy, a node schedules a broadcast for the first received copy of the flooding message. When the delay timer expires, the node may stop broadcasting the message if a responsibility condition is satisfied.

1.1 Related work

Pure flooding is inefficient. It leads to serious problems, including redundancy and collisions; so, it is not recommended for future applications (Tseng, 2001). Schemes in Cai et al. (2005), Wu & Li (1999), Pham & Choo (2008), Qayyum et al. (2002) and Lou & Wu (2004) have been proposed to reduce redundancy in flooding operations. However, these schemes either perform poorly in reducing redundant transmissions or require each node to maintain 2-hops neighbour information that incurs extra system overhead (Liu, H., 2007). Recently, there are several flooding schemes for the wireless environment that achieve very good results (Liu, H., 2007; Khabbazian, 2008; Le, 2008a; Le, 2008b; Liu, X., 2007). They are in the second category that uses 1-hop neighbour information to decide the forwarding nodes for a received flooding message.

A dominating set (DS) of a network is a subset of nodes such that every node in the network either is in the set or is a neighbour node of a node in the set (a CDS is a connected DS) (Wu, 1999; Stojmenovic, 2002; Dai, 2004). All forwarding nodes in a flooding operation form a CDS in the network, so the number of forwarding nodes that are required in the flooding operation is not less than the cardinality of minimal CDS (MCDS) in the network. Although computing MCDS is NP-hard, a ratio-8 approximation algorithm (R8A) exists (Wan, 2004). This scheme is used as a benchmark for comparison in Liu, H. et al. (2007), Khabbazian & Bhargava (2008), Le & Choo (2008a) and Liu, X. et al. (2007).

Liu, H. et al. (2007) propose a flooding scheme (we name it as 1HI) using the sender-based strategy. The mechanism of 1HI is summarized as follows: when a source node has a message to be flooded, based on the 1-hop neighbour geographical location information, it selects the next-hop retransmission nodes (together called the “forwarding set”) and attaches this set to the message header. After receiving a flooding message for the first time, all receiver nodes verify whether they are in the sender’s forwarding set. Every retransmission node computes its forwarding set in the same manner as the source node does. Then, based on the geographic location information, the receiver node optimizes its forwarding set by removing the nodes covered by the sender node and other lower-ID neighbouring retransmission nodes. After that, it relays the received message with the forwarding set attached. In this manner, the message eventually reaches all nodes in the network. The advantage of the sender-based 1HI flooding scheme is that it uses only 1-hop neighbour information; the protocol is easy to be implemented and has small overhead. However, this scheme has some disadvantages. First, the forwarding set is only locally optimized based on 1-hop neighbour information, and the number of forwarding nodes is relatively high. Second, the forwarding nodes are densely distributed along the network border. Most of the retransmissions broadcasted from network-border nodes are redundant, because their neighbours have already received this message from other previous-hop forwarding nodes.

The redundant transmissions of 1HI are the motivation for the work of Le & Choo (2008a) (called 2HBI). In this paper, the authors improve 1HI by using three rules proposed for deciding to remove a node from the forwarding set. Removing a node from the forwarding set reduces the number of nodes that retransmit a received flooding message. In evaluating performance, they show that their proposed improvement enhances 1HI. However, their scheme needs to collect 2-hops backward information to obtain better results. Collecting additional information could increase communication overhead and is inappropriate in mobile wireless environments where device nodes always move.

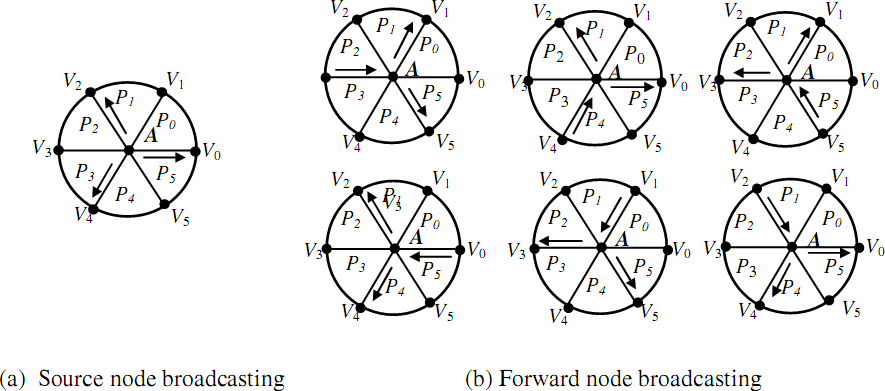
Another efficient sender-based flooding scheme is proposed in Liu, X. et al. (2007). The Vertex Forwarding scheme (VFS) guides the flooding procedure using a virtual hexagonal grid. Each node maps itself as a vertex of a hexagonal grid and keeps the knowledge of its adjacent vertex nodes, i.e., the neighbour nodes located at or nearest to adjacent vertices. Before a node broadcasts a message, it attaches the list of adjacent vertex nodes to the message. The nodes in the list are nominated as forwarding nodes. The main mechanism can be understood through the example in Figure 1. We consider the two cases where node A determines its forwarding nodes set F(A):

1. If A is a source node, three vertex nodes in the direction towards V₀, V₂, and V₄ are nominated as next hop forwarding nodes.
2. If A is a forwarding node, A selects two forwarding nodes from its forwarding candidates set.

The selection of forwarding nodes is based on direction information in the received flooding message. The efficiency of this scheme is very high; the number of forwarding nodes is close to the benchmark.

Figure 1. Forwarding nodes selection in Vertex Forwarding scheme.

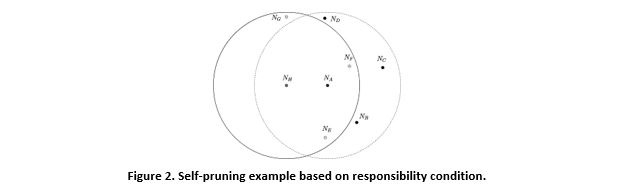
In a receiver-based flooding strategy, the Localized Broadcasting algorithm (LBA) proposed by Khabbazian & Bhargava (2008) achieves very high efficiency. The authors show that their proposed localized broadcast algorithms can guarantee a reasonable bound on the number of forwarding nodes. The proposed self-pruning algorithm achieves 100 percent delivery, as well as guarantees a constant approximation ratio to the optimal solution. The algorithm to compute the proposed responsibility condition has near minimal computational complexity. LBA is based on the following responsibility condition: node N_A is pruned (has non-forwarding status) if it is not responsible for any of its neighbours. Node N_A is not responsible for its neighbour N_B if N_B has received the message or if there is another node N_C such that N_C has received the message and N_B is closer to N_C than N_A. Figure 2 shows an example of the algorithm. Node N_A has six neighbours. Suppose that N_A has received a flooding message from N_H. Recall that N_A extracts the list of N_H’s neighbours from the received message. Therefore, it knows that N_E, N_F and N_G have received the message and N_B, N_C, and N_D have not. Based on the responsibility condition, N_A is not required to retransmit the message because: d(N_B, N_E) < d(N_B, N_E), d(N_C, N_F) < d(N_C, N_A) and d(N_D, N_G) < d(N_D, N_A) (or d(N_D, N_F) < d(N_D, N_A)), where d(N_A, N_B) is the Euclidian distance between two nodes N_A and N_B.

Figure 2. Self-pruning example based on responsibility condition.

1.2 Motivation

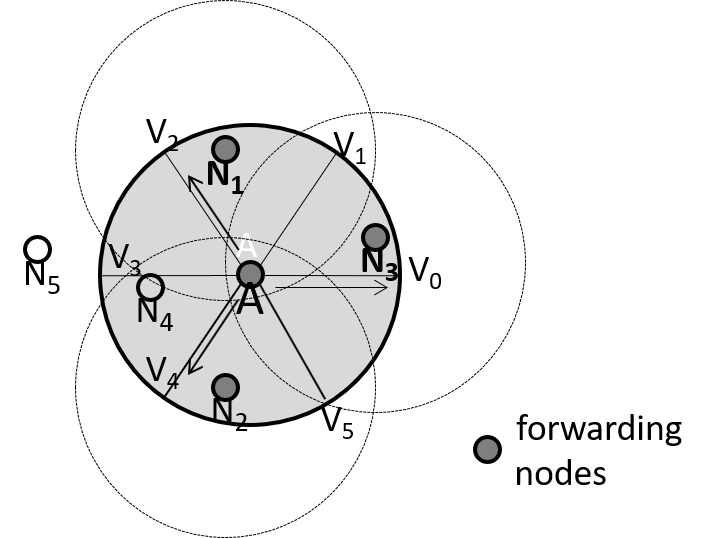
1HI is an efficient flooding scheme that achieves local optimality in two senses: the number of forwarding nodes and the time complexity for computing forwarding nodes. The authors also prove that their scheme has 100 percent deliverability for flooding. The performance of this scheme outperforms their previous work (Cai, 2005; Wu, 1999), but there are still many redundancies. The gap between the benchmark and 1HI is quite large. 2HBI, an improvement of 1HI, can achieve better results; however, the gap between the scheme and the benchmark is still large. Besides, 2HBI makes use of the information of 2-hops backward neighbours to improve 1HI. This is the trade-off as 2-hops information is unsuitable in mobile environments. With VFS, the performance of the proposed scheme is very high. The number of forwarding nodes is close to the benchmark. However, this scheme cannot guarantee 100 percent deliverability. The example in Figure 3 shows a situation in which a message cannot be flooded to the entire network. Suppose that node A has four neighbours: N₁, N₂, N₃, and N₄. Nodes N₁, N₂, and N₃ are chosen by node A as the forwarding nodes, and they should retransmit a flooding message received from A. However, node N₅ can communicate with node N₄ only, but node N₄ does not retransmit the received message due to not being in the forwarding set of node A. Therefore, in this case node N₅ cannot receive the flooding message. That means this message cannot be delivered to the entire network.

Figure 3. Missed delivery example in Vertex Forwarding scheme

LBA has impressive performance among the receiver-based flooding schemes. The authors show that their scheme outperforms 1HI. The number of forwarding nodes is slightly smaller than the benchmark (Wan, 2004). However, in the algorithm each forwarding node adds a list of its 1-hop neighbours’ IDs and positions to a broadcast message. This information is extracted and used to determine the next-hop node status (forwarding/non-forwarding). Even though the authors prove that the list of 1-hop neighbours can be replaced by a smaller set of representative neighbours, the piggyback information increases message size. Large message size consumes more energy in transmission and increases communication collisions. A high collision environment could consume more retransmission energy and affect the deliverability of the scheme also.

1.3 Our contribution

Motivated by the drawbacks of previous work, we propose a receiver-based flooding scheme for mobile ad hoc networks. Our proposed flooding scheme requires each node to keep only 1-hop neighbourhood information, including the node IDs and their geographic locations. The location information of each node can be obtained via GPS (Getting, 1993) or some distributed localization methods (Langendone, 2003) when GPS service is not available. We prove that our flooding scheme guarantees 100 percent deliverability for an ideal Media Access Control (MAC) layer, where no collision takes place.

Moreover, we consider our proposed scheme’s mobility handling applied to mobile environments. We also relax several system model assumptions, or replace them with practical ones, to improve the practicality of the proposed flooding scheme. Finally, we verify the performance and analytical results by computer simulation along with previous work. The simulation results show that the proposed flooding scheme outperforms previous work in many aspects.

The remainder of the paper is organized as follows. We propose an efficient flooding scheme for wireless ad hoc networks in Section 2. In Section 3, we discuss the simulation results of our flooding scheme, using the ns-2 simulator, and compare its performance to the best-known flooding algorithms. Finally, we conclude our work in Section 4.

2 The Proposed Flooding Scheme

We describe the assumptions of the proposed algorithm as follows: consider a wireless network as a collection of N nodes placed randomly in a plane; each node is equipped with an omni-directional antenna that has radio transmission range R. We call two distinct nodes neighbours if they are in transmission range of each other (that is, the Euclidean distance between them is less than or equal to R). We assume that each node is aware of its geographical location. Each node periodically broadcasts a short HELLO message containing its unique ID and its location to obtain the 1-hop location information of neighbour nodes.

2.1 Group forwarding scheme using 1-hop neighbours location information

The proposed flooding scheme follows a receiver-based strategy, so the general procedure for the algorithm is presented as Algorithm 1 (Khabbazian, 2008): when first receiving a copy of a flooding message, a node schedules a broadcast for a period. When the delay timer expires, the node considers whether it should retransmit the message if a specified responsibility condition is satisfied. During the delay timer, the node listens to the broadcast messages of neighbours to collect information needed for the responsibility condition.

Algorithm 1. General structure of self-pruning algorithms.

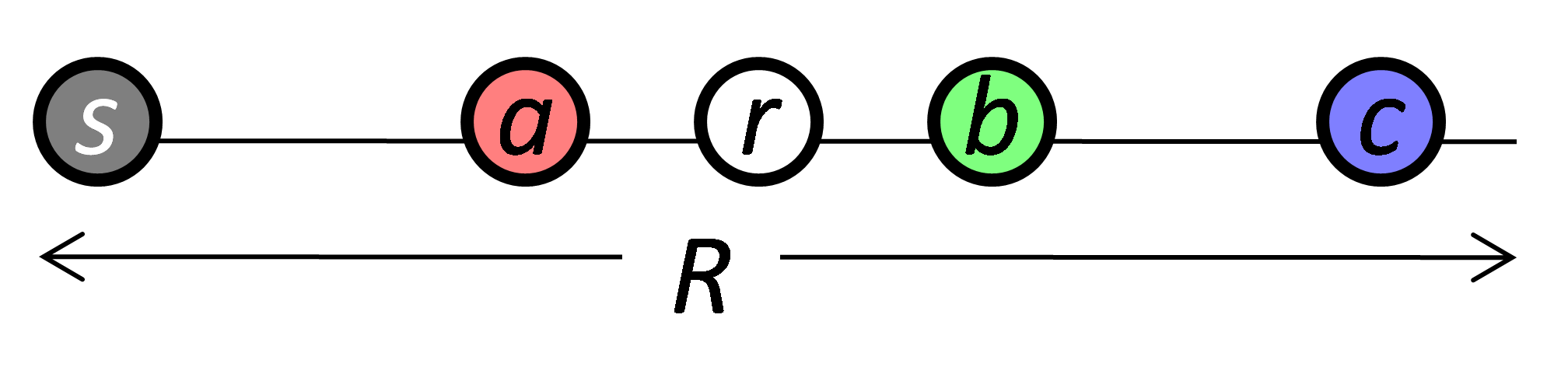
Algorithm 1 is a general procedure for a receiver-based flooding algorithm. The responsibility condition in our proposed flooding scheme originates from the following observation: if the identical area is covered by multiple nodes that receive the same message from the same sender s, the one farthest from s is the node that should retransmit the message. In Figure 4, we assume that node s broadcasts a message, nodes r, a, b, and c receive the message since they are in the transmission range of s. Only node c should retransmit the message because c can cover further areas compare to the retransmissions of nodes a, b, or r. By covering a larger area, we may reduce the number of forwarding nodes that need to broadcast messages to cover the entire network.

Figure 4. A scenario for node deployment

Using the above observation, we propose a novel flooding algorithm based on one round of neighbourhood information exchange. The proposed algorithm, Algorithm 2, is a simple modification of Algorithm 1.

Algorithm 2. The proposed flooding algorithm.

The difference between Algorithm 1 and Algorithm 2 is the order of the delay timer (line 4 in Algorithm 1 and line 5 in Algorithm 2, respectively). In Algorithm 1, we set the timer after the first time receiving a flooding message; then, the node collects the information in the overheard broadcast message of neighbours until the timer expires. The collected information is used to check the responsibility condition. However, in Algorithm 2, we set the timer only if the retransmission condition is satisfied. That means that only the nodes that need to retransmit the message set their timer. When the timer expires, nodes broadcast the received flooding message. This change reduces storage overhead in each node. In Algorithm 1, every node sets the timer and then collects the information and stores it in memory. However, in Algorithm 2, after receiving a flooding message, the node checks the responsibility condition immediately. Only some forwarding nodes should set the delay timer. Therefore, we can reduce storage and processing overhead that result in energy consumption. In the following section, we detail our proposed flooding algorithm.

A) Group division

To describe our proposed flooding scheme, we introduce the following definitions:

Definition 1. The coverage disk of node u, c(u), is a disk that is centred at u and whose radius is the transmission range of node u.

Since all neighbours of node u should be covered by c(u), we say “u covers v” or “v is covered by u” when v is a neighbour node of u.

Definition 2. The coverage area of a set of nodes A, C(A), is the union of coverage disks of nodes in A.

We simply state “the area is covered by A” if the area is within C(A).

Definition 3. The distance between two nodes, u and v, called d(u, v), is the Euclidian distance of those two nodes in the Cartesian plane: 

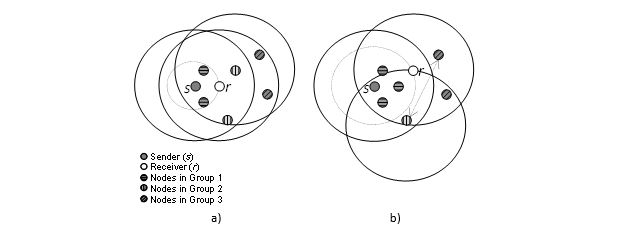
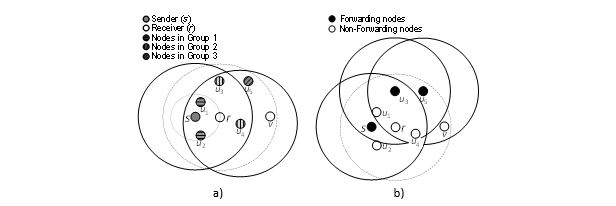
Suppose r is a node that receives a flooding message for the first time and s is the message sender (see Figure 5). Node r divides its neighbour nodes into three groups using 1-hop neighbour location information as follows:

Figure 5. An example of dividing neighbours into 3 groups

B) Relaying message

After dividing neighbour nodes into groups, node r checks the following condition to decide whether it should forward a received flooding message, or not.

In other words, node r should not retransmit a received flooding message if Group 3 is empty or if all nodes in Group 3 are covered by nodes in Group 2.

Nodes in Group 3 are inside the coverage area of node r; it is clear that, if all nodes in Group 3 are covered by nodes in Group 2, then the broadcasts by r and nodes in Group 2 will cause nodes in Group 3 to receive the same flooding message more than one time. We can eliminate this redundancy by letting either r or the nodes in Group 2 retransmit the message (but not both). In our proposed scheme, we choose nodes in Group 2 to be responsible for retransmitting the message, because the nodes in Group 2 cover an area at least as large as the coverage area of node r. So, if nodes in Group 2 broadcast the message, then more nodes can receive the flooding message. Besides, nodes in Group 2 are also further from the sender s than from node r to s, so they can cover a larger area compared to choosing r as the forwarding node.

Figure 6. Examples of checking the retransmission condition

We give an algorithm to determine the coverage of nodes in Group 3 by the nodes in Group 2. The following pseudocode (Algorithm 4) is used to determine the condition whether a node should forward a received flooding message. If node r receives a message from sender s as shown in Figure 5, it divides its neighbour nodes into 3 groups and then checks whether the retransmission condition is satisfied. Finally, if the retransmission condition is satisfied (return true), then r should retransmit the received message to its neighbours.

Algorithm 4. Computing the retransmission condition.

To illustrate the proposed flooding scheme, we consider the example in Figure 6. Suppose that s broadcasts a message and r receives the message from s. Node r divides its neighbours into three groups. Nodes in Group 3 of r are outside the transmission range of s so they cannot receive the message from s. In the situation of Figure 6(a), r knows that all nodes in Group 3 are covered by nodes in Group 2. Based on the retransmission condition, r is not required to retransmit the flooding message. For the case in Figure 6(b), there is one node in Group 3 that cannot be covered by any nodes in Group 2, so node r should retransmit the message to cover that node.

2.2 Efficiency improvement

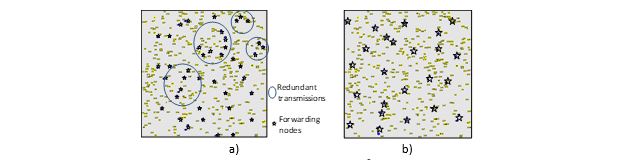
Figure 7. Broadcast nodes in a 1000x1000m² area with 400 nodes

Figure 7(a) illustrates an instance of using the proposed flooding algorithm to flood a message to an entire network where 400 nodes are randomly placed in a square area of 1000x1000m², and the node radio transmission range is set to 250m. From the figure, we observe that there are several broadcast nodes close to each other. Broadcast nodes stay close together; that is, the coverage areas overlap. The nodes inside this area receive the flooding message many times (duplicated messages) and then collisions are relatively high. Based on this observation, we propose Algorithms 5 and 7 to improve Algorithms 4 and 2, respectively.

Algorithm 5. Modification of computing retransmission condition.

Algorithm 6. Computing the second retransmission condition.

Algorithm 7. Improvement of the proposed flooding algorithm

From this point to the end of this paper, we consider Algorithm 7 and its dependency algorithms (Algorithms 3, 5, and 6) as our proposed scheme.Algorithm 7. Improvement of the proposed flooding algorithm.

In the proposed flooding scheme, when a node divides its neighbours into 3 groups (based on a flooding message received from a sender) or a node checks the coverage of two other nodes, we refer to the Euclidian distance. Two square operators and one square-root operator are required to calculate the distance between two nodes. Those operators are complex, consuming time and CPU instructions. In a mobile wireless environment, a device’s ability is limited, so computing the Euclidian distance many times consumes node energy. We make use of data structures to reduce computation overhead. We use a hash table H to store the pre-computed Euclidian distance between two neighbour nodes. On the first use of a distance value (i.e., the distance between nodes r and u), we calculate and store the value into the table (H(u) = value). Then, any later usage of the Euclidian distance between node r and its neighbour u can be retrieved by the function H(u).

2.3 100 percent deliverability

In this section, we prove that our proposed retransmission condition guarantees 100 percent deliverability. To prove this property, we assume that nodes are static, the network is connected, and the MAC layer is ideal, i.e., there is no transmission error.

Theorem. The retransmission conditions (Algorithms 5 and 6) guarantee that all network nodes receive the flooding message.

2.4 Relaxing some of the system assumptions

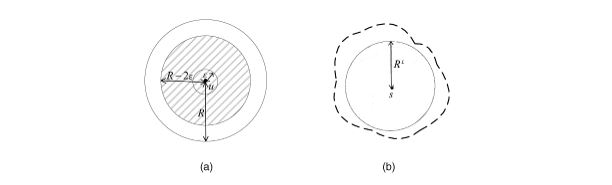
The proposed algorithm’s 100 percent deliverability is based on the assumptions made in Section 2.3. However, some of these assumptions are impractical. For example, the node location information may not be 100 percent accurate in real applications. Our proposed algorithm can be slightly modified to deal with imperfect location information. Suppose location information error is ε. For example, in Figure 8(a), the position of node u is u’s self-estimated location and u’s actual location is within a circle with radius of 2ε. We can simply make the valid coverage area of each node disk radius (R – 2ε) to compensate for this location error. In doing so, we can say that, if the distance between node r and node s is less than (R – 2ε), then node r can receive a message sent by s, because we have

Γ(r, s) – 2ε ≤ d(r, s) ≤ Γ(r, s) + 2ε,                                                                (1)

where Γ(r, s) is the exact distance between the nodes r and s (d(r, s) is calculated based on the inaccurate location information of the two nodes). If d(r, s) ≤ (R – 2ε), then

Γ(r, s) – 2ε ≤ d(r, s) ≤ Γ(r, s) + 2ε

⇔  Γ(r, s) ≤ R                                                                                                       (2)

That is, node r is in transmission range of node s. We modify Algorithm 3, 5 and 6 to group neighbour nodes and compute the retransmission condition under inaccurate position information by changing the function of checking the coverage of two nodes u and v (Algorithm 3 lines 2, 3, 4; Algorithm 5 line 5; and Algorithm 6 line 3, respectively) to:

v ∈ c(u) iff d(u, v) ≤ R – 2ε                                                                            (3)

Figure 8. Reducing coverage disk to compensate for the error in location and radius

Moreover, nodes may be mobile in ad hoc network environments, causing network topology to change. For the flooding scheme, each node maintains its neighbour information and sets the expiration status to the Euclidian distance in the Hash Table H. Using this method, we can handle mobility and our proposed flooding scheme can be applied to mobile environments.

3- Results and Discussion

To analyse the performance of our proposed flooding scheme, we compare it to three delivery-guaranteed flooding schemes: 1HI (Liu, H., 2007), 2HBI (Le, 2008a) and LBA (Khabbazian, 2008). We also compare it to the VFS scheme (Liu, X., 2007) that does not guarantee 100 percent deliverability. Table 1 shows the information of the target schemes for comparison.

Table 1. Five flooding schemes in simulation experiments

We run simulations under the ns-2 tools with the CMU wireless extension (CMU, no date). The simulation parameters are listed in Table 2.

Table 2. Applications in each class

The two-ray ground reflection model is adopted as the radio propagation model. The MAC layer scheme follows the IEEE 802.11 MAC specification. We use the broadcast mode with no RTS/CTS/ACK mechanisms for all message transmissions. The bandwidth of a wireless channel is set to 2Mb/s as the default. Notice that all of the schemes require the node to send a HELLO message to its 1-hop neighbours periodically, so this cost is ignored in our performance study. We analyse flooding efficiency in terms of the following metrics:

• The forwarding ratio is the ratio of forwarding nodes in the flooding operation to the total number of nodes in the network. The main objective of efficient flooding schemes is to reduce the number of forwarding nodes so that redundant transmission is minimized. Thus, this metric is an important criterion.
• Reducing the number of forwarding nodes in flooding would effectively reduce the number of signal collisions in the network. We also use the number of collisions to evaluate the efficiency of the flooding schemes. The number of collisions is defined to be the sum of the collisions experienced by each node before it receives a flooding message correctly.
• The delivery ratio is the ratio of the nodes that received packets to the number of nodes in the network for one flooding operation. Signal collisions eventually affect the delivery of flooding messages. Some nodes in the network miss the flooding messages, due to the large number of collisions. This metric is also important to further study algorithmic efficiency.

In each simulation run, we generate a specified number of nodes and randomly place them within a square area (using uniform distribution). The source that initiates a flooding message is randomly picked from network nodes. Only one flooding occurs at any one time (except in the experiments on delivery ratio). Four flooding schemes and the benchmark (Wan, 2004) are simulated and compared with our proposed scheme under the same conditions. The results presented in the following figures are the means from 100 separate runs. In the simulation of the performance on the forwarding ratio of the flooding schemes over different network densities, we fix the network size and vary the number of nodes. A specified number of nodes, from 50 to 1000, are randomly placed on a 1000x1000m² area. The transmission range is set to 250m.

Figure 7(b) illustrates an instance using the proposed flooding scheme, where R=250m, N=400 nodes, and the nodes are placed in a square area of 1000x1000m². Twenty-four nodes retransmit a flooding message to an entire network.

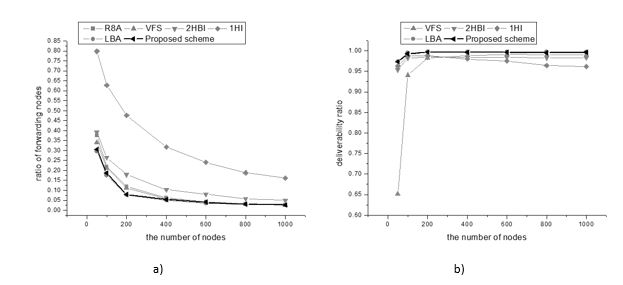
Figure 9(a) shows the ratio of forwarding nodes over the total number of nodes in the network. The performance of our flooding scheme is significantly better than that of 1HI and 2HBI for the number of forwarding nodes. We achieve similar performance compared to LBA and VFS.

Figure 9. Ratio of forwarding nodes and delivery ratio against number of nodes

In the delivery ratio experiments, network load is set to 10 packets/s; that is, the network generates 10 flooding messages per second on average. The delivery ratio is calculated over 100 seconds. Since 1HI, 2HBI, LBA and our proposed scheme guarantee full deliverability, the results show that these schemes achieve nearly 100 percent delivery ratio. In the high network load and node density cases, collisions cause missing packets, so the schemes cannot obtain 100 percent delivery, as shown Figure 9(b). For VFS, due to not guaranteeing delivery, the performance over a sparse network is very low (e.g., networks of 50 to 200 nodes in the area of 10⁶m²).

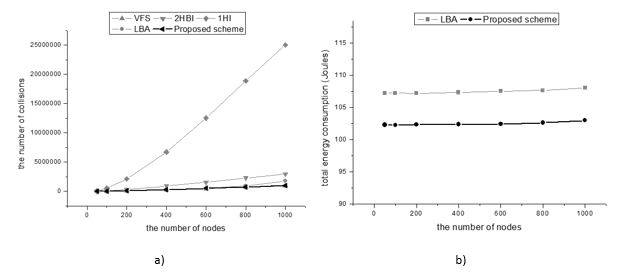
Figure 10(a) shows the experimental results on the number of collisions in the network. Due to the small number of forwarding nodes, LBA, VFS and our proposed scheme outperform 1HI and 2HBI. In a dense network, our scheme has fewer collisions compared to LBA, due to the varied sizes of the flooding messages. Our scheme requires smaller message size than LBA, so the number of collisions in dense networks is also smaller.

Figure 10. Ratio of forwarding nodes against number of nodes

Our proposed scheme outperforms 1HI and 2HBI (Figures 9 and 10(a)) in the case of 100 percent delivery-guaranteed flooding schemes. At the same time, our scheme achieves similar performance compared to LBA, since the two schemes are receiver-based and the method is somewhat similar. However, the approaches of the two flooding schemes differ. LBA selects the node nearest the non-covered node to retransmit the flooding message. In contrast, our proposed scheme is based on choosing the node that is furthest from the sender to be the forwarding node. Our approach is based on the observation that we want to cover an area farthest from the sender. We illustrate the difference between LBA and our proposed scheme in Figure 11. Assume that node s first broadcasts a message to its neighbours. Node r receives the message and decides not to retransmit because the responsibility/retransmission condition is not satisfied. In Figure 11(a), according to our proposed retransmission condition, node u₄ which is furthest away from sender s should take care of forwarding the received flooding message. In contrast, Figure 11(b) shows the situation of using the responsibility condition in the LBA scheme to decide forwarding node. Node u₃ should forward the flooding message because it is nearest to u₅, which is a node not covered by sender s.

Figure 11. Example of forwarding node selections in LBA (b) and our scheme (a)

The example above shows that different approaches bring different results (set of forwarding nodes) between LBA and our proposed scheme. Although LBA and our proposed flooding scheme have similar performance in terms of the number of forwarding nodes and delivery ratio, LBA requires piggybacking information in the broadcast message. This causes the message size to be larger. Transmission energy consumption depends on message length. Figure 10(b) shows the energy consumption of two flooding schemes. From the figure, we can see that energy consumption seems to be independent of the number of nodes. That is because the number of forwarding nodes does not change much when we vary the number of nodes in a constant network area. On the whole, our proposed scheme consumes less energy; and so our scheme can prolong network lifetime more than LBA.

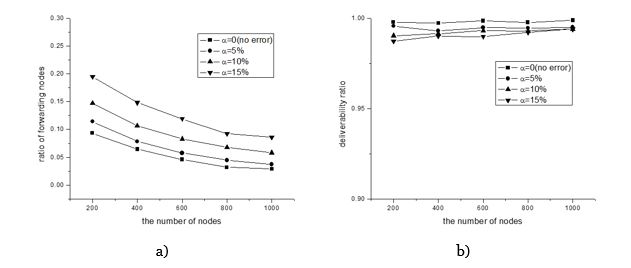
We also evaluate the performance of our proposed algorithm when there is inaccuracy in position information. We set the radio transmission range to R=250m and fixed the maximum position error to αR, where 0 ≤ α ≤ 0.15. Figure 12(a) shows the ratio of forwarding nodes for a given α. We see that the performance of the proposed flooding scheme just slightly degrades as the position error increases. Finally, we inspect the deliverability of the proposed scheme on the condition of uncertain position information (the network load is set to 10 pkt/s). As shown in Figure 12(b), the simulation results validate that, in spite of the existing uncertainty of position information, the proposed scheme achieves almost 100% deliverability.

Figure 12. Ratio of forwarding nodes and delivery ratio with uncertain position information

4- Conclusions

Traditional approaches to the implementation of flooding protocols suffer from excessive message redundancy, resource contention, and signal collision. In this paper, we address the efficient flooding problem in a wireless ad hoc network. The paper presents an efficient flooding scheme that uses only 1-hop neighbour location information and follows a receiver-based strategy. We show that the proposed flooding scheme can guarantee 100 percent deliverability. Simulation results validate that our proposed scheme uses fewer forwarding nodes, incurs fewer collisions, obtains a higher delivery ratio, and is more highly scalable than 1HI and 2HBI. The ratio of forwarding nodes of our proposed scheme is similar to VFS and LBA; however, our scheme is better than VFS in terms of delivery ratio and is better than LBA in terms of energy consumption – an important issue to prolong the network lifetime.

References

Abolhasan, M., Wysocki, T. and Dutkiewicz, E. (2004). ‘A Review of Routing Protocols for Mobile Ad Hoc Networks’, Ad Hoc Networks, vol.2, no.1, pp.1-22.

Cai, Y., Hua, K.A. and Phillips, A. (2005). ‘Leveraging 1-hop Neighborhood Knowledge for Efficient Flooding in Wireless Ad Hoc Networks’, Proc. of IEEE 24th Int’l Conf. on Performance, Computing, and Communications, pp.7-9.

CMU. (n.d.). Wireless Code from the UCB Daedelus and CMU Monarch Projects and Sun Microsystems, The Network Simulator, http://www.isi.edu/nsnam/ns.

Dai, F. and Wu, J. (2004). ‘An Extended Localized Algorithm for Connected Dominating Set Formation in Ad Hoc Wireless Networks’, IEEE Transactions on Parallel and Distributed Systems, vol.15, no.10, pp.908-920.

Getting, I. (1993). ‘The Global Positioning System’, IEEE Spectrum, vol.30, no.12, pp.36-47.

Haas, J. (1997). ‘A New Routing Protocol for the Reconfigurable Wireless Networks’, Proc. of IEEE 6th Int'l Conf. on Universal Personal Communications, pp.562-566.

Ho, C., Obraczka, K., Tsudik, G. and Viswanath, K. (1999). ‘Flooding for Reliable Multicast in Multi-hop Ad Hoc Networks’, Proc. of the Int’l Workshop on Discrete Algorithms and Methods for Mobile Computing and Communication, pp.64-71.

Khabbazian, M. and Bhargava, V.K. (2008). ‘Localized Broadcasting with Guaranteed Delivery and Bounded Transmission Redundancy’, IEEE Transactions on Computers, vol.57, no.8, pp.1072-1086.

Ko, Y.B. and Vaidya, N.H. (2000). ‘Location-Aided Routing (LAR) in Mobile Ad Hoc Networks’, Wireless Networks, vol.6, no.4, pp.307-321.

Langendone, K. and Reijers, N. (2003). ‘Distributed Localization in Wireless Sensor Networks: A Quantitative Comparison’, Computer Networks, vol.43, no.4, pp.499-518.

Le, T.D. and Choo, H. (2008a). ‘An Efficient Flooding Scheme Based on 2-hop Backward Information in Ad-hoc Networks’, Proc. of IEEE ’08 Int’l Conf. on Communications, pp.2443-2447.

Le, T.D. and Choo, H. (2008b). ‘PIB: An Efficient Broadcasting Scheme Using Predecessor Information in Multi-hop Mobile Ad-hoc Networks’, Proc. of the 2nd Int’l Conf. on Ubiquitous Information Management and Communication, pp.419-424.

Liu, H., Jia, X., Wan, P.J., Liu, X. and Yao, F.F. (2007). ‘A Distributed and Efficient Flooding Scheme Using 1-Hop Information in Mobile Ad Hoc Networks’, IEEE Transactions on Parallel and Distributed Systems, vol.18, no.5, pp.658-671.

Liu, X., Jia, X., Liu, H. and Feng, L. (2007). ‘A Location Aided Flooding Protocol for Wireless Ad Hoc Networks’, Proc. of the 3rd Int’l Conf. on Mobile Ad-hoc and Sensor Networks, pp.302-313.

Lou, W. and Wu, J. (2004). ‘Double-Covered Broadcast (DCB): A Simple Reliable Broadcast Algorithm in MANETs’, Proc. of the 23rd Annual Joint Conf. of the IEEE Computer and Communications Societies, pp.2084-2095.

Ni, S., Tseng, Y., Chen, Y. and Sheu, J. (1999). ‘The Broadcast Storm Problem in a Mobile Ad Hoc Network’, Proc. of ACM/IEEE 5th Int’l Conf. on Mobile Computing and Networking, pp.151-162.

Perkins, C.E. (2001). Ad Hoc Networking, Addison-Wesley Professional, Boston.

Perkins, C.E., Royer, E.M. and Das, S. (2003) ‘Ad-hoc On-Demand Distance Vector (AODV) Routing’, Internet experimental RFC 3561.

Pham, N.D. and Choo, H. (2008). ‘Energy Efficient Expanding Ring Search for Route Discovery in MANETs’, Proc. of IEEE ’08 Int’l Conf. on Communications, pp.3002-3006.

Qayyum, A., Viennot, L. and Laouiti, A. (2002). “Multipoint Relaying for Flooding Broadcast Messages in Mobile Wireless Networks’, Proc. of the 35th Annual Hawaii Int’l Conf. on System Sciences, pp.3866-3875.

Rendong, B. and Singhal, M. (2006). ‘DOA: DSR over AODV Routing for Mobile Ad Hoc Networks’, IEEE Transactions on Mobile Computing, vol.5, no.10, pp.1403-1416.

Sinha, P., Sivakumar, R. and Bharghavan, V. (2001). ‘Enhancing Ad hoc Routing with Dynamic Virtual Infrastructures’, Proc. of the 20th Annual Joint Conf. of the IEEE Computer and Communications Societies, pp.1763-1772.

Stojmenovic, I., Seddigh, M. and Zunic, J. (2002). ‘Dominating Sets and Neighbor Elimination Based Broadcasting Algorithms in Wireless Networks’, IEEE Transactions on Parallel and Distributed Systems, vol.13, no.1, pp.14-25.

Tseng, Y., Ni, S. and Shih, E.Y. (2001). ‘Adaptive Approaches to Relieving Broadcast Storms in a Wireless Multihop Mobile Ad hoc Networks’, Proc. of the 21st Int’l Conf. on Distributed Computing Systems, pp.481-488.

Wan, P., Alzoubi, K. and Frieder, O. (2004). ‘Distributed Construction of Connected Dominating Set in Wireless Ad Hoc Networks’, Mobile Networks and Applications, vol.9, no.2, pp.141-149.

Wu, J. and Li, H. (1999). ‘On Calculating Connected Dominating Set for Efficient Routing in Ad Hoc Wireless Networks’, Proc. of the Int’l Workshop on Discrete Algorithms and Methods for Mobile Computing and Communications, pp.7-14.